人有所不為,而后可以有所為�。
——《孟子》
1.為什么使用決策樹分析?
當項目需要做出某種決策���、選擇某種解決方案或者確定是否存在某種風險時�,決策樹(decision making tree)提供了一種形象化的�����、基于數(shù)據(jù)分析和論證的科學方法����,這種方法通過嚴密地邏輯推導和逐級逼近地數(shù)據(jù)計算,從決策點開始����,按照所分析問題的各種發(fā)展的可能性不斷產(chǎn)生分枝�����,并確定每個分支發(fā)生的可能性大小以及發(fā)生后導致的貨幣價值多少�,計算出各分枝的損益期望值�����,然后根據(jù)期望值中最大者(如求極小��,則為最小者)作為選擇的依據(jù)�����,從而為確定項目���、選擇方案或分析風險做出理性而科學的決策���。
2.決策樹分析有哪些作用?
決策樹分析清楚顯示出項目所有可供選擇的行動方案�����,行動方案之間的關(guān)系�,行動方案的后果�����,后果發(fā)生的概率,以及每種方案的損益期望值����;
使紛繁復雜的決策問題變得簡單、明了��,并且有理有據(jù)����;
用數(shù)據(jù)說話,形成科學的決策���,避免單純憑經(jīng)驗���、憑想象而導致的決策上的失誤。
3.怎么用�?
(1) 決策樹包含了決策點,通常用方格或方塊表示�,在該點表示決策者必須做出某種選擇;機會點���,用圓圈表示��,通常表示有機會存在�。先畫一個方框作為出發(fā)點,叫做決策點�����;
(2) 從決策點向右引出若干條支線(樹枝線)�����,每條支線代表一個方案���,叫做方案枝���;
(3) 在每個方案枝的末端畫一個圓圈,叫做狀態(tài)點���;
(4) 估計每個方案發(fā)生的概率�����,并把它注明在在該種方案的分支上����,稱為概率枝;
(5) 估計每個方案發(fā)生后產(chǎn)生的損益值,收益用正值表示,損失用負值表示�;
(6) 計算每個方案的期望價值,期望價值=損益值x該方案的概率���;
(7) 如果問題只需要一級決策,在概率枝末端畫△表示終點�,并寫上各個自然狀態(tài)的損益值; (8) 如果是多級決策���,則用決策點□代替終點△重復上述步驟繼續(xù)畫出決策樹��,如圖1所示���。 (9) 計算決策期望值,決策期望值=由此決策而發(fā)生的所有方案期望價值之和�����;
(10) 根據(jù)決策期望值做出決策�。
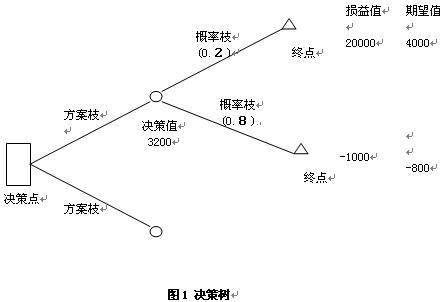
圖1 決策樹
4.舉例:
某承包商向某工程投標,計劃采取兩種策略:一種是投高標�����,中標機會為0.2,不中標機會為0.8�����;另一種是投低標�,中標與不中標機會均為0.5。投標不中時����,則損失投標準備費5萬元。根據(jù)下表數(shù)據(jù)�,用決策樹做出決策。
|
方案 |
效果 |
可能獲利
(萬元) |
概率 |
|
高標 |
好 |
500 |
0.3 |
|
一般 |
300 |
0.5 |
|
賠 |
-100 |
0.2 |
|
低標 |
好 |
350 |
0.2 |
|
一般 |
200 |
0.6 |
|
賠 |
-150 |
0.2 |
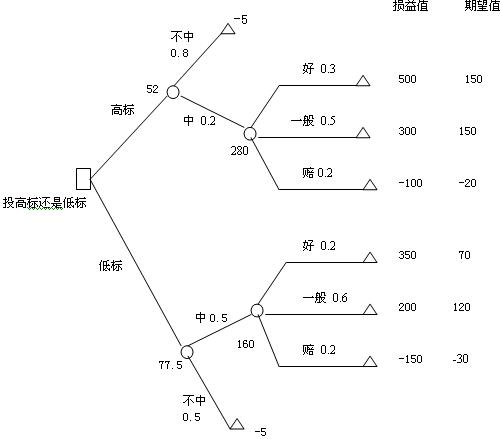
計算的結(jié)果表明���,
高標:
500×0.3+300×0.5-100×0.2=280萬�,280×0.2-5×0.8=52萬�����;
低標:
350×0.2+200×0.6-150×0.2=160萬�����,160×0.5-5×0.5=77.5萬;
最大損益期望值為77.5萬,也就是上說若投高標��,可能最多只能賺到52萬����,而若投低標則有可能賺到77.5萬,故應(yīng)采取低標策略。 

項目經(jīng)理勝任力免費測評PMQ上線啦�!快來測測你排多少名吧~
http://www.vanceur.cn/pmqhd/index.html
